
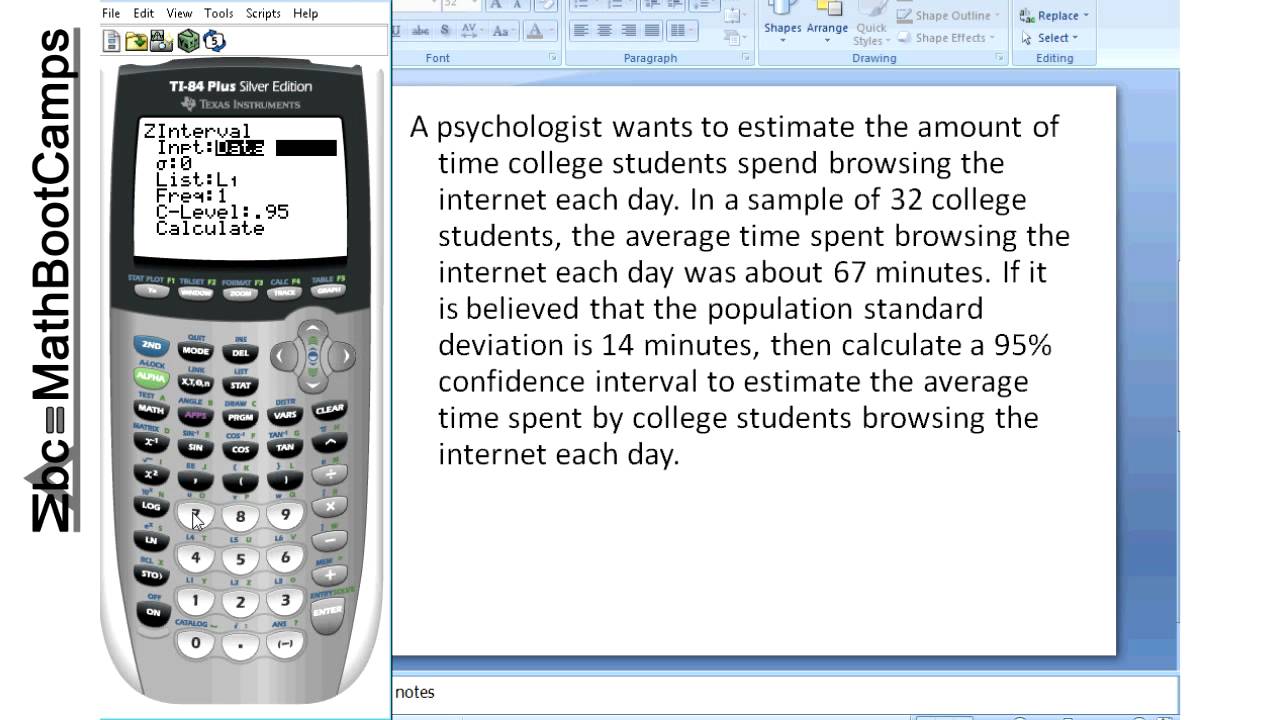
The t α value for 24 with a confidence level of 95, we obtain the value of 2.064. Since the sample size is small (below 30), we take the sample size and subtract 1 to get the degrees of freedom (df). The resultant confidence interval will be computed and displayed.Ĭalculating the confidence interval for a given group can be useful for any science, including electronics.Ĭalculate the 95% confidence interval for a data set given its mean cost is $193.73, its standard deviation is $26.73, and its sample size is 25. To use this calculator, a user simply enters in the mean, standard deviation, the sample size of the data, and the confidence interval s/he wants toįind out, and clicks the 'Calculate' button. We calculate the lower estimate by the formula, lower estimate= mean - (standard deviation)(value of t α). The value of t α is obtained by looking up the value based on a table. Once we obtain this value, we calculate the upper estimate of the interval by the formula, upper estimate= mean + (standard deviation)(value of t Sample size, according to the formula, σ x= σ/√n. The confidence interval calculator calculates the confidence interval by taking the standard deviation and dividing it by the square root of the The confidence interval of 99.9% will yield the largest range of all the confidence intervals. The confidence level, we get a larger and larger range. The confidence level, we get a larger range of values to increase our confidence that the mean will be in the subset.
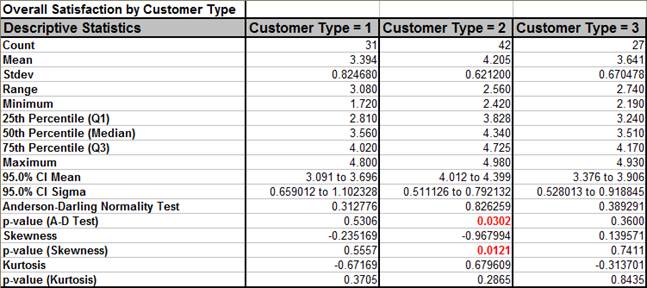
This means that we are 95% confident that the mean is between 18.9 and 47.9.Ī confidence level of 50% will yield the shortest interval because it is the smallest and the least precise of all the confidence levels. If we do so, we will get the interval of 18.9 to 47.9. We want to calculate the 95% confidence intervalįor this data. This calculator allows us to calculate the confidence interval for a group of data for 50%, 60%, 70%, 80%, 90%, 95%, 98%, 99%, 99.8%, and 99.9% confidenceįor example, let's say we have a sample size of 32, with a mean of 33.4 and a standard deviation of 42. The confidence interval allows us to quantify how confident we can feel a group of data is from its mean value. Standard deviation, and sample size for the data unit.
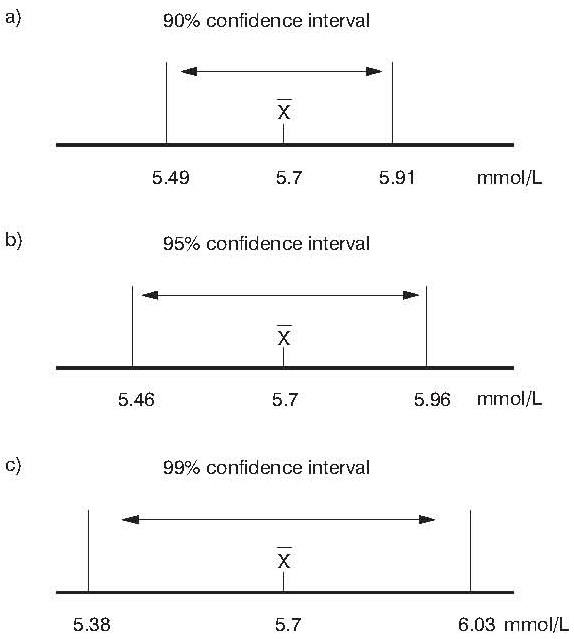
The probability of a Type II Error can be calculated by clicking on the link at the bottom of the page.This Confidence Interval Calculator calculates the confidence interval for group of data, given we have the mean, These can be solved using the Two Population Calculator. Sometimes we're interest in hypothesis tests about two population means. The calculator on this page does hypothesis tests for one population mean. Confidence intervals can be found using the Confidence Interval Calculator. If the hypothesized value of the population mean is outside of the confidence interval, we can reject the null hypothesis. Hypothesis testing is closely related to the statistical area of confidence intervals. Ideally, we'd like to reject the null hypothesis when the alternative hypothesis is true. A Type II Error is committed if you accept the null hypothesis when the alternative hypothesis is true. Ideally, we'd like to accept the null hypothesis when the null hypothesis is true. A Type I Error is committed if you reject the null hypothesis when the null hypothesis is true. The observed difference in conversion rate isnt big enough to declare a significant winner. There are two types of errors you can make: Type I Error and Type II Error. Variation Bs observed conversion rate was higher than variation As conversion rate ().You can be 95 confident that this result is a consequence of the changes you made and not a result of random chance. When conducting a hypothesis test, there is always a chance that you come to the wrong conclusion. To switch from σ known to σ unknown, click on $\boxed$, reject $H_0$. Furthermore, if the population standard deviation σ is unknown, the sample standard deviation s is used instead. Use of the t distribution relies on the degrees of freedom, which is equal to the sample size minus one. If σ is unknown, our hypothesis test is known as a t test and we use the t distribution. If σ is known, our hypothesis test is known as a z test and we use the z distribution. The formula for the test statistic depends on whether the population standard deviation (σ) is known or unknown. The first step in hypothesis testing is to calculate the test statistic.


 0 kommentar(er)
0 kommentar(er)
